🔢 수학 속 놀라운 규칙과 📐 기하학의 세계를 쉽고 흥미롭게 소개합니다. 숫자에 숨겨진 원리와 공간 구조의 아름다움을 함께 살펴보세요.
🔍 Discover the fascinating world of math through 🔢 simple yet surprising rules and 📏 elegant geometric structures. Explore the hidden logic behind numbers and shapes.

The Fascinating World of Mathematical Rules and Geometric Structures
1. 모든 자리 숫자의 합이 9의 배수이면, 그 수는 9로 나누어떨어진다.
If the sum of all the digits of a number is a multiple of 9, then the number itself is divisible by 9.
· 예: 2 + 5 + 2 = 9 → 252는 9로 나누어짐.
· Example: 2 + 5 + 2 = 9 → 252 is divisible by 9.
2. 모든 자리 숫자의 합이 3의 배수이면, 그 수는 3으로 나누어떨어진다.
If the sum of all the digits of a number is a multiple of 3, then the number itself is divisible by 3.
· 예: 1 + 2 + 3 = 6 → 123은 3으로 나누어짐.
· Example: 1 + 2 + 3 = 6 → 123 is divisible by 3.
3. 숫자를 뒤집어서 원래 수와 뺀 결과가 9의 배수이면, 그 수는 9의 배수이다.
If you reverse the digits of a number, subtract it from the original, and the result is a multiple of 9, the original number is also divisible by 9.
· 예: 432 - 234 = 198 → 198는 9의 배수 → 432도 9의 배수.
· Example: 432 - 234 = 198 → 198 is a multiple of 9 → therefore, 432 is divisible by 9.
4. 세 자리 수에서 앞뒤 숫자를 바꾼 뒤 원래 수에서 빼면 항상 99의 배수가 된다.
If you reverse the digits of a three-digit number (switching the hundreds and units digits) and subtract the reversed number from the original, the result is always a multiple of 99.
· 예: 835 - 538 = 297 → 99 × 3
· Example: 835 - 538 = 297 → 297 = 99 × 3
5. 마지막 자리수가 5인 2자리 수의 제곱은 첫자리 수 × (첫자리 수 + 1) × 100 + 25이다.
The square of any two-digit number ending in 5 can be calculated using this formula: First digit × (First digit + 1) × 100 + 25.
- 예: 65 × 65 = 6 × 7 × 100 + 25 = 4225
- Example: 65 × 65 = 6 × 7 × 100 + 25 = 4225
- 이것을 식으로 표시하면 (10a + 5)² = 100a² + 100a + 25 = 100a × (a + 1) + 25 = a × (a + 1) x 100 + 25
- In algebraic form: (10a + 5)² = 100a² + 100a + 25 = 100a × (a + 1) + 25 = a × (a + 1) x 100 + 25
📚 참고자료 / 이미지 출처
본문 내 이미지 출처: Pixabay 제공 무료 이미지 (출처 링크)
'수학으로 배우는 영어' 카테고리의 다른 글
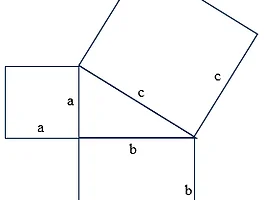
| 📐 피타고라스의 정리 (0) | 2025.05.05 |
|---|---|
| 🧮 5x5 마방진 만들기 (0) | 2025.04.27 |
| 🧮 3x3 마방진 (3x3 Magic Square) (0) | 2025.04.10 |